为什么这里不等式的范围在平方后变为大于等于零,可以严格推导吗?

平方数非负。在不等式中因此可比,于是这些都是实数,实数取平方必然非负。初中反复强调的重点。
请记牢。
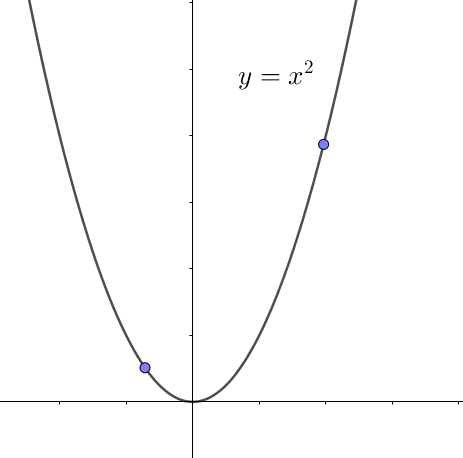
你画个抛物线 图像就明白了.
 严格证明就用
严格证明就用 隔开分段啊. 很容易证明的呀.
x^2≥0,就这么简单。
可以由实数体系 的公理化定义的域公理和序公理推出。
(F) 域公理 : 略
(O) 序公理: 是有序域
(O1)序的传递性: x?y, y?z?x?z.(O2)序可以决定元素: x?y, y?x?x=y.(O3)全序关系: 对任意的 x 和 y, x?y 或者 y?x, 二者必居其一 (可以都成立) .(O4)与加法相容: x?y?x+z?y+z.(O5)与乘法相容: x?0, y?0?xy?0.证明:
(1)lemma1 :
证:
(2) lemma2 : 证:i)
则 直接由公理(O5)得到
ii)若 ,则
,又由lemma 1,
得
再根据公理(O3) 于是 lemma成立2.
取
于是 证明完毕。
参考:于品数学分析讲义——实数的公理化定义
实数的平方都大于等于0,如果你是高中生,问如何推导的话,对高中生来说没什么严格推导的必要......
如果你看到之后不觉得左边是0,你可能是这样的想的:
的
如果你确实是这样想的,不妨画个抛物线y=x2,看看x在区间[-0.5,1.5]的时候,y的值域到底是什么范围。