扫雷到底怎么玩？

　　如题

　　方格中的数字，表示围绕这个方格的八个格子内的地雷数目

　　扫雷这款游戏，是基于在隐藏方块中掺入雷方块，将雷区周围的空方块点掉，会漏出空白格和数字格，而数字格则是重点，数字格会表达出相接触的周围八个方格中有几颗雷，当然仅仅知道周围方块有几颗雷还是不行，因为需要用除了识别数字格以外的三个判断方法，第一是固定形式，简单的来说，扫雷这款游戏中数字格所对应的雷方块的分布，在一些特定的局势下，是有着固定的排布，比如一排数字格中有数学1旁边的数字格是数学2再旁边的数字格是数字1，那么两个数字1所直接横边对应的方块就是雷，这是一个比较常见的固定排布，还有一些比较难以不借助示意图讲解的固定排布。

　　第二个是逻辑推理，这是最重要的，简单的来说就是利用数字格和周围局势以及剩余未标记雷数推算而积累的经验。

　　第三就是数雷数，一般用在数字格无法准确的表达周围哪个方块是雷的时候用的，还可以用在，已经到了场上没有多少还未点开的方块时用，计算一些地方到底还是都可能有雷。

　　扫雷就是记住各种“定式”。所谓定式就是对出现特定的数字局能立马反应出来周围那些个是雷，那些个不是雷。比如下面的局部，你能推出那些个必定是雷吗？注意，要训练成条件反射那样，不是思考推理。

　　还有出现概率局部（逻辑推理不出的局面），就靠运气马上点开此局部。爆了就从来。不要绕着去点其他部分。最后还得靠猜。。

　　常见定式秒开，你的水平是高级难度的150秒左右。

　　简单地讲一下我使用的简单方法。

　　首先，每个数字都宣布着它周围到底有多少个雷，这个周围，就是以它为中心的九宫格，而很多时候，我们都会看到，周围的所有空格刚好就是雷的总数：

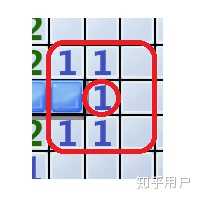
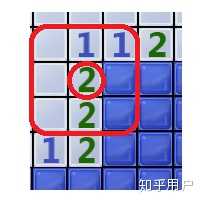
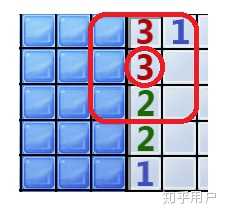
　　对于这些情况，直接就可以进行标记，是属于很确定的情况，其它的还有

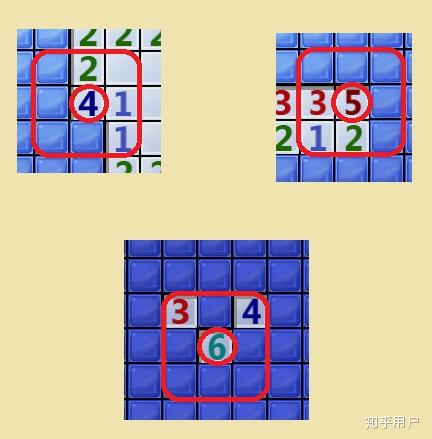
　　展示一下其中一个的真实情况：

　　而其他情况，则是依靠着推理的方式进行审定：

　　上面这个图，以 为中心的九宫格， 的最下面的 指出了一个雷的位置，从而用旗子进行标记，然后 下面的 则根据已经标记出来的旗子而指出了一个没有雷的位置，从而把以 为中心的九宫格的所有雷都审定出来了。

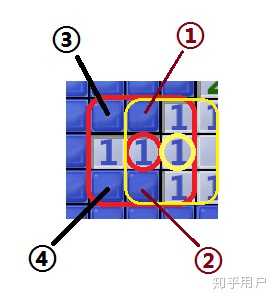
　　对于这一个图，黄色圈的 在说，①和②其中一个格子必有一个雷，而另一个没有雷；红色圈的 则依靠前面这个推理知道，③和④都不会有雷，从而可以把③和④都点开。

　　对于这个图，如果红色框的最上面两个空格都有雷，那么会跟黄色圈矛盾，因此红色框的最上面两个空格最多只能有 个雷；但红色圈的 已经说红色框内有 个雷，因此， 位置必然有雷，所以在 的位置放红旗。

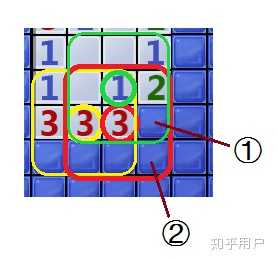
　　此图中的绿色九宫格内已经指出①位置有 个雷，而黄色九宫格则刚好指出 个雷，把它们都标记出来，这时就可以看出，红色框内刚好有 个标记出的雷，因此知道②的位置没有雷。

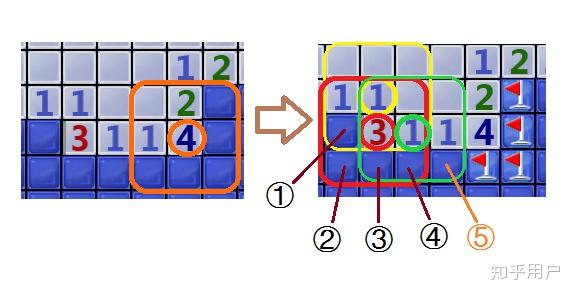
　　在这个情况中，我们想知道以 为中心的九宫格的 个空格中，到底哪 个位置有雷。易知①位置有 个雷；而绿色框内的中心数字 在说明，③和④只是其中一个有雷，这是因为，如果③和④都没有雷，那么红色框则无法凑足 个雷，矛盾，而如果③和④都有雷，则与绿色框的中心数字 矛盾，因此，只能③和④只是其中一个有雷；既然③和④其中一个有雷，那么就会导致⑤这个位置没有雷，因此可以把⑤点开；从而就可以知道，这时候， 的九宫格只剩下 个空格，因此这 个空格都有雷，把它们如图标记上旗子。

　　最后，还有一些让人十分无奈的情况，它很多时候都是在最后一刻才揭晓出来，有的时候则是中途即已经揭示出来，也就是无法通过任何判断来知道有雷无雷：

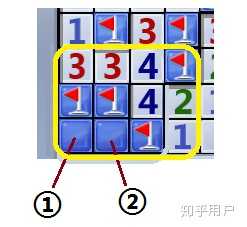
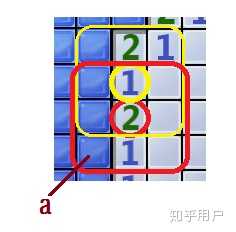
　　很明显，此图中，黄色框内的所有信息已经是一个封闭的系统了，所以我们只需要看这个圈内的信息能不能推出①和②有没有雷。可以看出，②还是能够判断出来的，它是有雷的；但是对于①这个位置，则没有任何信息告诉我们，到底它是有雷还是没有雷。

　　这种情况当然可以依靠雷的总数来最后判断出这个地方是否有雷，但如果有两个地方同时出现这种情况，而且只剩下最后 个雷的标记，那么就没有任何办法判断出是否有雷。