如何看待「长尾科技」的新作《什么是高中物理》？
「长尾科技」在《什么是高中物理》（原文：什么是高中物理？）里用 4.5 万字基本上把高中物理脉络理清楚了，从零建立了高中物理图像，并尝试剖析了出题人的逻辑，大家怎么看这篇文章？觉得会产生什么影响？按照文章的套路能搞定高中物理么？高中物理到底应该怎么学习，怎么去教？物理学霸、学神们能不能来谈谈自己的心得体会？培养物理学家的素养和高考拿高分到底冲不冲突？大家在学习高中物理的时候又有什么故事，能不能一起来谈一谈高中物理的那些事？
更新：基于这篇文章的同名书籍《什么是高中物理》（长尾科普系列丛书-01）已上市，觉得在手机上看不太方便，或者想让自己和朋友家的中小学生也看看的，书里还有很多在文章里限于篇幅没有讲的东西：
很多同学初中时很喜欢物理，觉得物理很简单也很有意思。但一到高中就感觉跟不上了，感觉跟自己以前认识的物理不是一个东西，不再那么直观，也不再那么简单有趣。
于是，在一些可以自由选择高考科目的地方，大量考生纷纷放弃物理，“弃考物理”曾一度成为热门话题而引发全国关注。
但是，物理学作为自然科学的基础学科，研究大至宇宙，小至基本粒子等一切物质最基本的运动形式和规律。要铸大国重器，少了物理怎么行？要是都不学物理，那不用三体人，自己就把自己的科技树锁死了。
于是，许多地方改变了高考策略，改为理科生必选物理。
这种改变在长尾君看来无可厚非，理科生要是不学物理，那还叫啥子理科生？但是，追根溯源，我们还是得问：为什么很多原本喜欢物理的人，一到高中就不喜欢物理了？仿佛一到高中，物理就变得又难又无趣，跟初中物理不是一个物种似的。
其实，物理一直都是很美并且很有趣的。
但是，高中物理和初中物理的确有点不一样。如果不能及时认识到这点，还一直用初中物理的思维学习高中物理，那肯定会各种不适应，觉得物理又难又无趣，那就不好玩了。
在这篇文章里，长尾君就来跟大家好好聊一聊，一起看看高中物理跟初中物理到底有什么区别？看看如何理清高中物理框架，如何建立清晰的物理图像。
如果你初中刚毕业，希望你能迅速调整自己的思维；如果已经高二高三，希望这个对你重新理解物理，对你复习备考有帮助；如果还是初中生、小学生，打个预防针也不错~
高中物理和初中物理有一个非常大的不同：很多物理问题在初中只要你做定性的分析，到了高中就要你做定量的计算。
从定性分析到定量计算是一步非常大的跨越。
在初中，我们只需要定性地分析那些热学、光学、力学、电磁学的现象。
分析水为什么会变成冰和水蒸气？为什么会听到回声？为什么苹果往下落，水往低处流？为什么磁铁会同性相斥、异性相吸？为什么筷子在水里会折断？
这种定性分析跟日常生活联系得非常紧密。我们每学一点物理知识，就仿佛揭开了大自然某处的面纱，好奇心和求知欲在这个过程中得到了极大的满足。
这种初见物理的朦胧美，一如初见的恋人。人生若只如初见，那谁都可以跟物理谈恋爱。
恋爱期间我们可以靠对电、磁、力、热、光等领域的新鲜感来维持关系；婚后就要靠对柴米油盐酱醋茶、房贷、车贷精打细算来维系生活。
于是，进入高中，我们就要对力学、电磁学等领域进行精确的定量计算。
初中我们只要知道为什么苹果会往下落；高中就要能算出苹果1秒钟下落了多高，2秒后的速度是多少。
初中我们只要知道电荷同性相斥，异性相吸；高中我们就要知道两个电荷相距1米，它们的吸引力和排斥力到底有多大。
初中我们只要知道电荷在电场中会加速运动；高中我们就要算出电荷的运动的具体轨迹。
这样，大家明白从初中物理到高中物理到底发生什么了么？
是的，从恋人变成了夫妻。话题从以前的梦想环游世界，变成了计算下个月的房贷、车贷有多少，计算年终奖发多少可以去欧洲旅游。
现在你知道为什么很多人初中喜欢物理，到了高中就突然不喜欢物理了吧？没错，跟很多人想一直谈恋爱不想结婚一个道理~
但是，物理学是研究一切物质的运动形式和规律的学科，我们当然不能只满足于对物理现象做一些定性分析。
我们从自然界总结出了各种物理定律，再利用这些定律去改造自然。这可是一丁点差错都不能有的，必须进行精确的定量计算。
那么，做定量计算就不简单也不美了么？
如果我们可以算出每个物体的运动情况，对宇宙中所有物体的运动规律都了如指掌。这种开了上帝视角，这种宇宙万物尽在我心中的感觉，绝不是那种初见的朦胧感能比的。
如果你把物理图像都看清楚了，把物理框架建起来了，你会发现高中物理的定量计算其实一点也不难（我以前在小号写过一篇《如何引导初中生做定量的物理计算？|长尾谈话录》，感兴趣的可以先看看）。
好，接下来，我们就回到物理学的起点，再重新认识一次物理。
宇宙万物都在运动和变化之中，物理学就是要研究它们的运动变化规律，研究它们为什么会运动，怎样运动？
我们能看见物体，是因为光子跑到眼睛里来了；我们能听见声音，是因为声波通过空气传入了耳朵；我们能接听电话，是因为有电磁波在给我们传递信息；至于苹果熟了会下落，推下椅子，椅子就会动就更不用说了。
如果没有运动，世界将是一片死寂，那也没物理学啥事了。
既然运动是如此的普遍和显然，那物体为什么会运动呢？
咋一看，这个问题好像很好笑，但仔细一想，你会发现它远没有想象的那么简单和理所当然。
为什么苹果往下落，热气球却往天上飞？我推一下椅子，椅子就往前走，一松手椅子就停了，难道有外力物体才会动？一个铁球比一根羽毛落得更快，是因为铁球更重一些么？
这些问题是如此的平常，但回答起来却异常的困难。古希腊时期很多自然哲学家都思考过这些问题，但答案都不太令人满意。
比如你想，我推椅子，椅子就动了。这个好理解，通过接触传递力也很容易接受。
但是，苹果下落时，并没有东西跟它接触啊，为什么它还会运动呢？热气球上升时，也没有东西跟它接触，为什么它也跟着运动？
而且，为什么苹果往下运动，热气球却往上运动呢？难道说重物都往下落，轻物都往天上飞？
这里，肯定有些同学想说：苹果下落是因为受到了向下的引力，热气球上浮是因为受到了向上的浮力。
很多家长在回答孩子的问题时，也喜欢直接这样甩答案。这答案虽然没错，但它过于从天而降。孩子们通过这种答案只能获得一个零碎的知识点，无法了解背后的知识体系，也无法体会科学是如何建立起来的。
古希腊人对自然界进行了细致地分析和深入的哲学思考，最后形成了一套自洽的自然哲学体系。
在这个过程中，出力最多、处于核心地位的是亚里士多德，我们姑且把这一整套看待世界的观点称为亚里士多德世界观。
这套观点认为，地球是宇宙的中心，日月星辰都围着地球转。
地球上的物质由水、火、土、气四种基本元素组成。土元素天然会向宇宙中心运动（所以石头会掉下来），水元素也天然向宇宙中心运动，但这一趋势比土元素弱（所以水也会往下运动，但在土的上面），气元素天然向水和土以上运动（所以水里的气泡会往上面冒），火元素有一种天然远离宇宙中心的趋势（所以火在空气中向上燃烧）。
一个物体如果趋于静止，要么是组成这个物体的元素已经达到了它在宇宙中的自然位置（比如水和土到了地球中心），要么是被其他东西（如地球表面）挡住了。
一个静止的物体会一直保持静止，除非它有其它的运动来源（要么是自己趋于宇宙自然位置的运动，要么是外界给了力，比如我推桌子）。
其它观点我就不一一列举了，大家看了之后有什么感想？
你有没有感觉，虽然这些观点在今天看起来很“幼稚”，但它却是一套自洽的体系。它能把自己的话圆回来，不会自相矛盾；它也能解释为什么物体会运动，能比较好的解释古人看到的各种现象。
甚至，对小孩子来说，这一套更符合“常识”，更容易被理解和接受。
但是，这并不是科学，而是自然哲学，真正的科学此时还没有诞生。亚里士多德世界观还要统治欧洲近两千年，一直到伽利略的出现。
伽利略认为，我们不能只对运动做定性的分析，还要做定量的计算。
我们应该用数学定量地描述物体的运动，再用实验去验证，而不再讨论诸如物体的目的、本性这种形而上，无法量化的东西。
这就意味着，伽利略放弃了古希腊以来的自然哲学传统，正式创立了以数学和实验为根基，以“描述自然现象”为任务，而不是尝试去“解释自然现象本质”的现代科学。
重物会下落，那我就看看它是怎么下落的，第1秒下落了多高，第2秒下落了多高，找找规律。
你说物体越重下落得越快，那我就来做实验，看看一个重铁球和一个轻铁球是不是如此。
你说所有的物体达到它的自然位置之后就会趋于静止，那我就来做实验看看到底是不是这么回事。
做了一堆实验之后，伽利略大惊失色，他发现事情根本不是原来想的那样。感觉靠不住，我们得用实验说话。
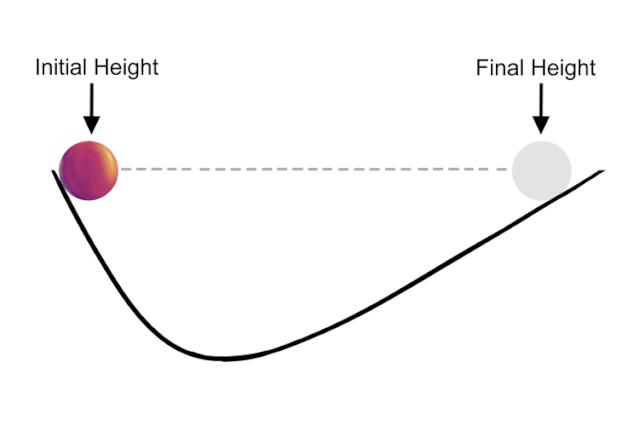
首先，伽利略从一系列斜坡实验中发现：一个物体是否运动，跟它有没有受力没有直接关系，运动不需要外力来维持。
他设计了一个光滑的斜坡，发现不管我从左边多高的地方放下小球，小球基本上都能回到右边相同高度的地方。
进一步，我们减小右边的坡度，让右边越来越平。那么，为了回到同样的高度，小球就得运动更远的距离。
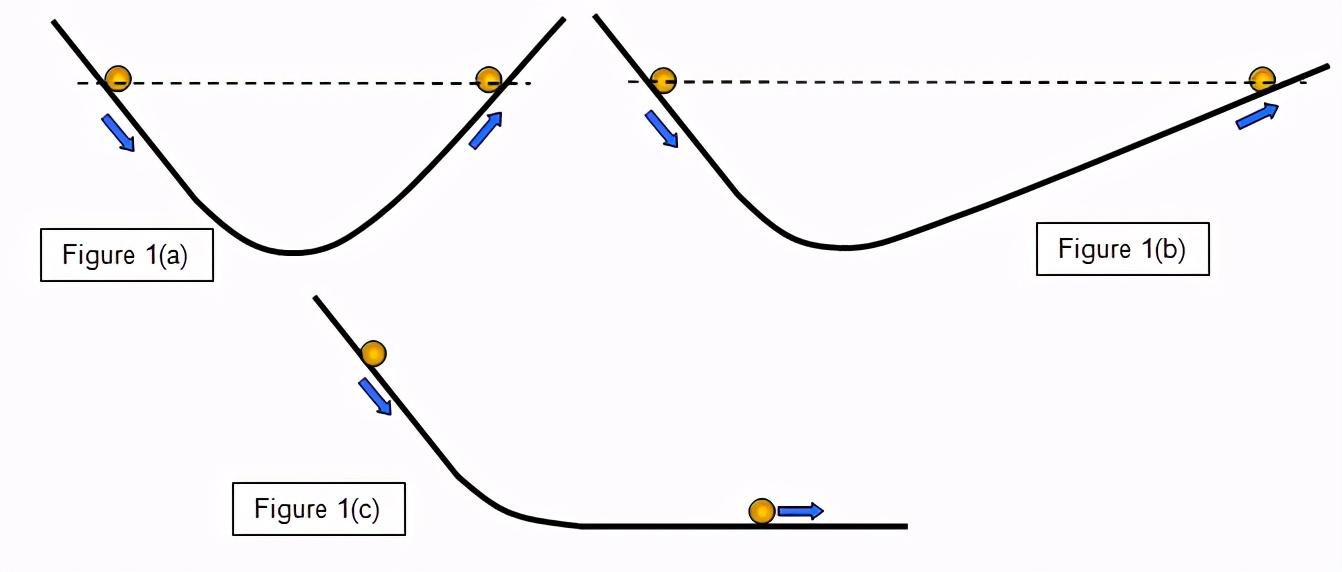
最后，我把右边的斜坡完全放平，那右边就变成了一个平面，高度永远不变了。这样，无论小球运动多久，运动多远，都不可能再回到左边的高度。
永远回不到左边高度的意思是：小球会一直匀速直线运动下去（假设地面绝对光滑）。
这就像在溜冰场，地面越光滑，你就能一次性滑得越远。如果地面绝对光滑，你就会永远停不下来，直到碰到其它障碍物。
通过这个实验，伽利略发现运动本身并不需要力来维持，物体不受任何外力作用时也能保持匀速直线运动的状态。
那么，力的作用到底是什么呢？我用力推椅子，椅子的状态确实改变了，也确实好像是我用的力气越大，椅子的速度就越大。
伽利略针对这些问题做了进一步研究，最后发现：力不是维持物体运动的原因，而是改变物体运动状态的原因。
也就是说，维持物体的运动不需要力，但改变物体的运动就需要力了，力还是非常有用的。
小钢球在绝对光滑的地面上能一直匀速直线运动，速度的大小和方向都不变。但如果我用力推小球，小球的速度就会改变。
伽利略的工作非常重要，他不仅开创了现代意义上的科学，指明了科学研究的基本方法。也身体力行，发现了大量物体运动的基本规律，给后人指明了方向。
接下来，牛顿就在这些工作的基础上，建立了一整套描述物体运动的理论。这就是大名鼎鼎的牛顿力学，也是高中物理的核心。
牛顿力学有三大运动定律，理解了伽利略的发现，你就会觉得这些定律非常自然。然后你会发现：通过这些定律，我们竟然真的可以描述物体的各种运动。
所谓定律，就是科学家通过做各种实验，从实验现象里总结出来的规律，它的正确性由实验保证。定律是无法通过数学公式“推导”或者“证明”出来的，那些证明出来的叫定理。
数学家会预设一些最基本的公理（比如欧式几何的5条几何公理），然后从这些公理出发，通过逻辑演绎证明各种定理，构建起一座座坚固的数学大厦。
因为数学并不用对现实世界负责，所以公理的选择具有相对的任意性。你可以选这几条作为公理，推出一套数学体系；也可以选那几条作为公理，推出另一套数学体系。
只要体系内部不自相矛盾，都是可以的。就像欧式几何和非欧几何虽然在第五公设针锋相对，但它们却可以和谐共存。
但是，物理学是要对现实世界负责的，所以根基不能随便选。它一定要符合实验，符合从自然界观测的结果。
而定律就是从各种实验现象里总结出来的规律。因此，有些物理学家就以定律为根基，建立了一套理论体系，比如牛顿力学。
还有一些物理学家以原理为根基建立了理论体系，比如爱因斯坦的相对论。甚至，整个物理学都可以从最小作用量原理导出来。
原理并不是从某个具体实验总结出来的具体定律，而是大家从大量物理规律中总结出来的一些普遍成立的东西。这些原理对物理定律的形式有非常严格的限制，成了“管定律的定律”。
这样说，大家就明白牛顿的三大运动定律是什么地位了吧？它们是牛顿力学的根基，决定了牛顿力学的基本骨架。
下面，我们就来看看这三大定律到底都说了什么。
牛顿第一定律：物体在不受力，或者受到的合外力为0时，它将保持静止或者匀速直线运动（即速度的大小和方向都不变）。
牛顿第一定律也叫惯性定律，它告诉我们“运动并不需要力来维持”。如果物体受到的合外力为0，那它之前是什么速度，后面就依然是什么速度。
为什么它还有一个名字“惯性定律”呢？惯性在英文里跟惰性是同义词，就是懒的意思。
所以，惯性定律就是说所有的物体都很“懒”，像懒猪一样，都不愿意主动改变自己的运动状态。
如果我现在没动，那就打死不动，除非你用力推我；如果我现在有一个速度，那就一直以这个速度无脑前进，除非有力拦着我。
喜欢科幻电影的朋友肯定对这个画面不陌生：一个宇航员不小心弄断了连接飞船的绳子，然后大家就只能眼睁睁地看着这个宇航员以这个速度飘向太空深处。
因为太空中没有其它外力拦住他，所以他就只能遵守惯性定律“懒”下去，一直以这个速度飘走（虽然他是如此的不愿意）。
这也说明，没有力，宇航员照样可以运动，力的确不是维持物体运动的原因。
那么，力的作用到底是什么呢？伽利略在后半句里说了：力是改变物体运动状态的原因。
也就是说，虽然运动本身不需要力来维持，但是，如果你想改变运动状态，比如宇航员不想飘向太空深处，想回到飞船，这就需要一个外力来拉一把。
好，知道力可以改变物体的运动状态之后，我给你一定的力，你的速度能改变多少呢？
想要把这个账定量地算清楚，我们就需要牛顿第二定律。
怎么算呢？
首先，既然力可以改变物体的速度，那我们首先就得找一个物理量来描述物体速度的变化。比如，汽车现在的速度是2m/s，1秒后变成了4m/s，那它的速度就在1秒钟之内变化了4-2=2m/s。
为什么汽车的速度会变化呢？
当然是发动机的牵引力让汽车的速度发生了改变，换成马车就是马的拉力让车的速度改变了。既然速度发生了改变，那肯定就有什么力作用在它身上。
那么，力的大小跟速度的变化有什么关系呢？是力越大，速度的变化就越大么？
咋一看好像没问题。我用两匹马拉车，1秒内可以让马车加速2m/s；如果有四匹马，或许1秒内就能让马车加速4m/s。
但是，就算我只有一匹马，如果时间给够，比如60秒，那马车完全有可能增加更多的速度。
所以，光比速度的变化量是不公平的，我们还要限定时间：在一定的时间内（比如1秒钟）让物体的速度变化越大（也就是速度变化得越快），才能说明受到的力越大。
因此，我们有理由相信：合外力越大，物体的速度变化得越快。而单位时间内物体速度的变化量，正是加速度的定义。
也就是说，我们用加速度这个物理量来描述物体速度变化快慢的程度。
如果物体的速度不变，那它的加速度等于0；如果物体的速度在1秒内从2m/s增加到了4m/s，那它的加速度就是2m/s2；如果物体的速度在2秒内从1m/s增加到了7m/s，那么它的加速度就应该是（7-1）/2=3m/s2。
好，现在我们知道了：物体受到的合外力越大，它的速度变化得越快，加速度越大。
那么，还有其它影响加速度的因素么？同样是一匹马，一个拉自行车，一个拉大卡车，你觉得它们的加速度会一样么？
很显然，物体的加速度不仅跟合外力有关，还跟质量有关：质量越大，同等拉力下获得的加速度越小，反之越大。
有这样的铺垫，牛顿第二定律就呼之欲出了。
牛顿第二定律：物体的加速度a跟物体受到的合外力F成正比，跟物体的质量m成反比，写成公式就是F=ma。
于是，我们就引出了牛顿力学里最重要的一个公式，整个高中物理都可以说是在学习F=ma在各种情况下的应用。
牛顿第二定律也让我们有了一个全新的视角来审视“质量”这个概念。
惯性定律不是说“万物都很懒”么？没有外力推，一个个都打死不改变自己的运动状态。
但是，虽然大家都很“懒”，但是“懒”也分三六九等。有的物体是轻微的懒，轻轻一推就改变了运动状态；有的是极品的懒，用八抬大轿都抬不动。
那么，如何判断一个物体是一丢丢懒，还是非常懒呢？答：根据质量。
因为牛顿第二定律告诉我们，一个物体的质量越大，同等外力下产生的加速度就越小，即运动状态变化得越慢，这不就是更懒的意思么？
所以，质量就成了一个衡量物体运动状态改变难易程度的物理量。质量越大，越胖，越不想动，想想好像真的好有道理。
从这个角度，大家再来感受一下牛顿第二定律F=ma：外力（F）想改变物体的运动状态（a），但质量（m）越大，物体越懒，越坚持自我，越难被外力（F）所改变。
所以，内心越强大，越难被外界的诱惑所改变；质量越巨大，越难被外力的压迫所改变~
最后，再顺带看一下牛顿第三定律。
牛顿第三定律：相互作用的两个物体作用力和反作用力大小相等，方向相反（牛顿的原话是“每一个作用都有一个相等的反作用”，并没有提到“力”。但因为我们在讨论牛顿力学，所以教材里就直接用作用力和反作用力来表述，方便理解）。
这很好理解，比如我用力推一下墙，就会感觉墙也用力推了一下我，这两个力大小相等，方向相反。
好，理解了牛顿的三大运动定律，就理解了牛顿力学的根基，然后就可以分析万物的运动情况了。
宇宙万物到底是如何运动的？隐藏在运动背后的规律又是什么？之前有很多人回答过这些问题，但答案都不太令人满意。
现在，牛顿同学递交了他的答卷，一份令人非常满意的答卷。
答卷的主体就是牛顿三大运动定律，它的核心思想是：如果物体不受外力（或者合外力为0），它将一直保持原来的速度。如果合外力不为0，它的速度就会改变，即具有一定的加速度。想知道加速度到底是多少，就用牛顿第二定律F=ma去计算。
例如，为什么茶杯在桌子上静止不动？因为茶杯受到了一个向下的重力，和一个来自桌面的向上的支持力，这两个力大小相等方向相反。
因此，茶杯受到的合外力为0，所以茶杯就静止不动。
为什么我推一下椅子，椅子就动了呢？
因为我推椅子时，椅子在水平方向上受到了一个推力，合外力不为0。根据牛顿第二定律F=ma，这个合外力会让椅子产生一个加速度，于是椅子就动起来了。
为什么松手之后，椅子会慢慢停下来呢？
因为松手之后，推力没有了，椅子在水平方向上受到的合外力就只有来自地面的摩擦力（摩擦力一直都在，但之前比推力小）。摩擦力与椅子运动的方向相反，因此会产生一个让椅子减速的加速度，于是椅子就慢慢停了下来。
为什么苹果熟了会往下落呢？因为苹果没熟时，苹果受到了一个向下的重力和一个树枝向上的拉力，这两个力大小相等方向相反。所以，苹果受到的合外力为0，于是保持静止。
苹果熟了以后，树枝承受不了苹果的重量，就跟苹果分离了。于是，苹果受到的合外力就只有向下的重力。根据F=ma，苹果会有一个向下的加速度，因此苹果会加速往地面掉落。
为什么月亮会围着地球转呢？因为地球和月亮之间有一个万有引力，月亮受到的合外力就是这个引力。根据F=ma，月亮会有一个加速度，这个加速度不断改变速度的方向，让月亮围着地球转。
为什么电荷在电场中会运动呢？因为电荷在电场中会受到一个电场力，此时电荷受到的合外力就是这个电场力。根据F=ma，电荷会有一个加速度，于是电荷开始加速运动。
为什么会潮起潮落？因为月亮对海水有一个吸引力，这个吸引力会给海水提供一个加速度。当地球转动时，这个加速度也会跟着变化，于是……
这些例子我可以给你无限列举下去，但是你发现没有，我用来解释物体为何这样运动的“套路”都是一样的：都是先看物体受到了什么力，把合外力F找出来，再利用F=ma求出物体的加速度a，最后根据加速度分析物体的运动情况。
来来去去就这三板斧，一套组合拳包打天下，这就是牛顿力学。
所以，大家现在明白为什么牛顿第二定律F=ma这么重要了么？
因为这个公式的左边代表了物体的受力情况（合外力F），右边代表了物体的运动情况（加速度a），F=ma则把物体的受力情况和运动情况紧密地联系在了一起。
物理学要研究万事万物的运动情况，牛顿第二定律F=ma告诉你：小伙子，想知道物体是怎么运动的吗？那就去看看它受到了什么力吧。我传你一套祖传秘籍F=ma，只要你告诉我它受到了什么力，我就能告诉你它将如何运动。
有了牛顿第二定律的神助攻，我们研究万事万物如何运动的宏伟目标，就变成了研究万事万物都受到了什么力。
那么，世界上都有些什么力呢？面对各种各样的力，我们又要如何研究呢？
答案是：先分类，再各个击破。
我们先对所有的力逐一盘问：你导致物体的运动状态发生了这样的改变，你是什么力？
就像提着一袋垃圾走向分类垃圾桶时，经常也会收到的问候一样：你是什么垃圾？
然后，我们就坐在力的分类桶前面开始审查：你让苹果加速下落，是引力，去1号桶；你让月亮围着地球转，还是引力，也去1号桶；你让杯子无法穿透桌面掉下去，是支持力，本质上是电磁力，去2号桶；你让原子核里的质子、中子没有因为电磁斥力散架，是强力，去3号桶……
科学家就这样对各种运动现象逐一考察，找出它们背后的力，然后对这些力进行分类。
最后你猜结果怎么着？
最后，大家惊奇地发现：只要4个桶，不用成百上千，也不要十个八个，只要4个桶就能把人类迄今为止发现的所有力都装进去。
什么意思？意思就是我们对各种力进行分类，发现力的数量虽然多，但种类却很少，只有区区4种（不过科学家还是觉得多，他们巴不得只有1种才好），这4种力分别是：引力、电磁力、强力、弱力。
这就非常有意思了。
你看啊，牛顿第二定律告诉我们：如果你想研究物体的运动情况，就去分析它的受力情况。知道了受力情况，就能通过F=ma求出它的加速度，进而知道它的运动情况。
一开始看到这段话，很多人可能觉得这是在转移矛盾，觉得这无非就是把锅从运动情况甩到受力情况这边来了，并没有实质性地解决问题。
但是，我现在告诉你：虽然物体的运动情况很复杂，但决定物体运动的力，却只有屈指可数的4种。
这样，问题的性质就从根本上发生了变化：如果总共只有4种力，那我完全可以把它们一个个弄清楚啊，毕竟4个又不多。
深入研究4种力，回报是掌握一切物体的运动情况，这买卖，太值了！
当然，你可能会疑惑：真的只要4种力就能搞定一切？有那么便宜？我读书少，你不要骗我。
科普人不打诳语，不仅如此，我还有一个更好的消息：虽然我们说有4种力，即引力、电磁力、强力、弱力。但是，强力和弱力只在原子核级别才有显著作用，日常生活中一般感觉不到它们的存在，高中物理也不会讲。
于是，你在高中会碰到的所有力，就只有引力和电磁力两种。怎么样？4种变2种，有没有双十一五折大甩卖的感觉？
接下来，我们就来仔细看看这两种力，看看为什么说日常生活中只能感觉到引力和电磁力。
引力，又叫万有引力。
万有的意思很明显，就是说这种力是普遍存在的，任何两个有质量的物体之间都有这样一种力，谁也跑不掉（在牛顿力学里先这样理解，以后学了广义相对论，你会对引力有更加深刻的认识）。
这个意思很直白，就是说万物之间都会相互吸引。
你可能会疑惑：不会吧，万物之间都有吸引力？我和同学、课桌、教室之间也有？为什么从来没感觉到？
引力的确是万有的，别说跟你同学，就是跟看长尾公众号的手机，跟绣花针之间都引力。只不过这些力都太小，察觉不到。
为什么引力小呢？当然是因为质量小。你的体重在引力眼里不值一提，想感受引力，就得选个质量大的。
比如，你可以选择教学楼，你和一栋楼之间的引力就比两个人之间的大多了（想想教学楼的质量是你同学的多少倍）。不过，这个引力还是太小，依然感觉不到。
那再大一点，选择喜马拉雅山。很可惜，还是太小。
你可能要发飙了，我和这么大一座山之间的引力还小？你怕不是来忽悠我的吧。还嫌质量小，那我把整个地球选给你好不好？
好，那我就不客气地签收了！这次你选对了。
引力虽然是万有的，但是它非常微弱，我们需要地球这个级别的物体才能直观感受到它的存在。
地球和我们之间的引力深深影响着每个人的生活，它给了我们安全感，也给了我们恐惧。它让地球不会分崩离析，也俘获了月亮的心……
你可以想一想，为什么你每次跳起来之后都会落回地面？
你可能觉得这理所当然，或者从来就没想过，似乎“每个物体都会往下落”是天经地义的事情（就像亚里士多德说的“XX天然有向地球中心运动的趋势”一样）。
但是，你想想惯性定律，万物都是“懒”的，人也一样。
如果没有外力影响，物体会一直保持原来的运动状态。原来是静止的，后面就一直静止；原来有一个速度，后面就一直以这个速度匀速直线运动。
我们跳起来时，速度是指向天上的，跳起来后慢慢减速，到了最高点速度为0，然后开始反向加速下落。
整个过程中，速度的大小和方向都发生了明显的变化，这就表明跳跃时肯定受到了其它外力的影响，这个力让我们的速度发生了改变。
但是，我们跳起来后明明没有跟任何东西接触，那这能是什么力呢？答案是引力，是我们和地球之间的万有引力。
任何两个物体之间都有引力，地球和地面物体之间当然也是。你可以把地球想象成一个巨大的吸铁石，它对地面上的任何东西都有强大的吸引力，所以高处的物体总会往低处走。
于是，你跳起来，又被吸回来；苹果会被吸到地面，高处的水被吸到低处；你提着一袋东西觉得重，那是因为地球想把这袋东西吸过去，但你“死死拽着”不放，你在跟地球拔河；月亮一直围着地球转，也是因为被地球吸住了，想跑跑不掉……
这些，都是地球引力干的，它吸引着一切，感知极强。
因为我们生活在地球，从小就感受着来自地球的引力，所以早已见怪不怪。
但是，如果哪天你到了月球，因为月球的引力比地球小很多，你可能轻松一跳就是两层楼高；如果在外太空，可能轻轻一跳，就永远下不来了。
长尾君当年学习引力时，还解开了一个困惑我多年的谜题，内心倍感舒畅，这里也分享一下。
从小我就知道人类生活在地球表面，那问题就来了：我住在地球“上面”，头朝上，那住在地球另一面的人岂不是脚朝上？为什么他们没有掉下去？
直到学了万有引力，我才恍然大悟：原来大家都是被地球吸住的！
根本就没有什么绝对的上下，也不是上面的东西天生就要往下落，而是大家都被地球吸得往地心方向跑而已。
好，到这里，相信大家对引力就有一个概念了。
但这还远远不够，虽然我知道苹果下落、月亮围着地球转都是引力造成的，那引力具体是怎么影响它们的呢？
这个地球引力到底会使苹果以多大的加速度下落？1秒后苹果的速度是多大，2秒后会下落几米？它会使月亮以多大的周期围着地球转？
如果不把这些细节搞清楚，我们也不好意思说弄懂了它们的运动情况。
说白了，我们必须能定量算出两个物体间引力的大小，然后才能用牛顿第二定律F=ma算出具体的加速度，进而分析物体的运动细节。
引力的规律要如何找呢？
前面说了，引力非常微弱，地面物体之间的引力非常小。想通过观测它们来总结引力的规律，怕是行不通。
所以，我们把目光转向了天上。月亮围着地球转，地球和其它行星围着太阳转，一些大的行星（比如木星和土星）还有一堆卫星围着它们转，这些肉眼可见的天文现象可都是引力主导的啊。
于是我们夜观星象，把星体的运动轨迹都记录下来（一个叫第谷的人做得极好）。然后分析它们的运动轨迹，从中找出一些星体的运动规律（第谷的学生开普勒发现了行星运动的三大定律）。最后根据这些定律，利用数学和物理知识反推出让星体这样运动的力应该具有什么样的性质。
这一步，很多科学家都在走，但牛顿凭借他逆天的数学和物理才华（唯一一个同时稳居数学、物理Top3的人），第一个走出了迷宫，给出了描述引力的精确定律，并用它成功解释了当时一切跟引力相关的运动现象。
这一仗，牛顿大获成功，这个能精确描述引力的定律，被称为万有引力定律。
牛顿是如何得到这个定律的，这里不细说。我们先来直观地感受一下，来猜一猜这个定律应该长什么样。毕竟它号称能精确描述万有引力，我们看看它的描述跟我们的直观感受是否冲突。
大家知道，任何两个物体之间都有引力，而且质量越大，引力越大。
那么，引力就只跟质量有关么？太阳的质量比地球大得多，为什么我们没有被太阳吸走？答案当然是：因为地球距离我们更近。
所谓强龙压不过地头蛇，我的地盘我做主，任何势力都有他的范围，引力亦然。所以，除了质量，引力还应该跟距离有关。
而且，容易想象，引力跟质量、距离的关系，一定是质量越大，引力越大；距离越大，引力越小。
这不是什么问题，真正的问题是：它们之间定量的关系到底是怎样的？我把质量增大到原来的2倍，引力会增大多少？把距离扩大为原来的2倍，引力又会减小多少？
只有把这个关系搞清楚了，才能精确地计算引力，才算搞定了引力。
先来看引力和质量的关系。
假设有两个1kg的铁球，它们之间有一定的引力。那么，如果其中一个铁球的质量从1kg增加为2kg，你觉得引力会变成多少？是原来的2倍（1×2），3倍（1+2），还是其它什么的？
理论上来说，应该是2倍，也就是说质量之间应该是乘法关系。
因为我可以把2kg的铁球看成两个1kg的铁球，那每个1kg铁球的引力就和原来的一样，新的引力自然就是原来的2倍。
所以，两个物体之间的引力F应该和这两个物体的质量m1、m2的乘积成正比。其中任何一个物体的质量增加为原来的多少倍，它们之间的引力就增加为原来的多少倍。
引力和质量的关系好说，真正困难的是和距离的关系。
假设两个小球相距1米，现在它们之间的距离扩大为2米。那么，它们之间的引力会减小为原来的多少呢？是原来的1/2，1/4，还是1/8什么的？
有人说你可以去做实验啊，看看把两个小球之间的距离增加一倍以后，它们之间的引力会缩小为原来的几分之一。
但是，引力的实验不好做啊。
因为引力非常微弱，地面上两个物体之间的引力很难测量。而且，引力是万有的，我们很难屏蔽其它物体对实验的影响。
引力有显著作用的地方，还是在天上。开普勒就是从星体运动的轨道数据里发现了行星运动三大定律，牛顿从这里打开了思路，最终发现（其实胡克、哈雷等人也发现了）引力跟距离的平方成反比。
也就是说，如果两个物体之间的距离变为原来的2倍，它们之间的引力就减小为原来的1/4；距离变为3倍，引力就减小为原来的1/9。
其实，平方反比定律在自然界非常常见。
大家想想圆的周长公式C=2πr，周长跟半径（即半径的1次方）成正比。圆的面积公式S=πr2，球体的表面积公式S=4πr2，面积跟半径的平方（2次方）成正比。圆球的体积公式V=4πr3/3，体积跟半径的立方（3次方）成正比。
发现没有，周长跟半径的1次方成正比，面积跟半径的2次方成正比，体积跟半径的3次方成正比。
而现实世界是3维的。这就意味着，如果有个东西爆炸了，它释放出来的能量就会以球面的形式向外扩展。
比如，某个爆炸产生的冲击波1秒钟传播1千米，那么，2秒后这个冲击波就会向空间各方向传播2千米，组成一个半径为2千米的2维球面。
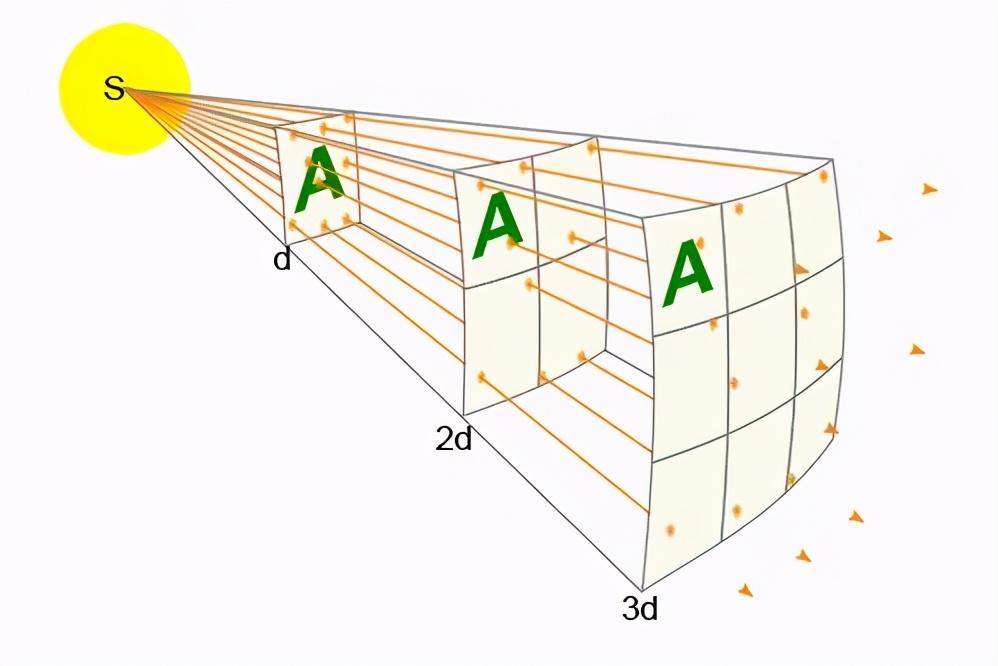
球的表面积公式是S=4πr2，于是，我们可以粗略的认为：爆炸源的能量每时每刻都被平均分给了4πr2个部分，它跟半径r的平方有关。
这就是各种平方反比定律更深层次的来源。
同样，如果我们的空间是4维的，你就会看到各种立方（3次方）反比定律，这也是科学家们检验是否存在高维空间的一种办法。
好，理解了这些，引力跟距离的平方成反比就非常正常了。
于是，我们就知道了：两个物体之间的引力F跟两个物体的质量m1、m2成正比，跟它们之间距离r的平方成反比。
写成公式就是：
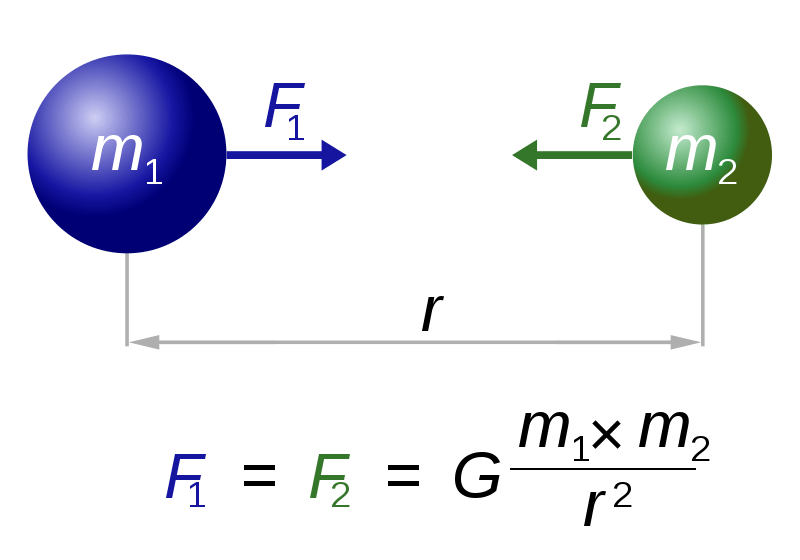
这就是大名鼎鼎的万有引力定律，是牛顿力学里描述引力的东西。
图中F表示引力，因为引力是相互的，你吸引我，我也吸引你。而且这种吸引大小相等、方向相反，图里就用F1、F2分别表示。
因为质量越大，引力越大，所以分子就是两个物体质量m1和m2的乘积。因为空间是3维的，所以引力的大小跟距离的平方成反比，于是分母是r2。最外面的G是万有引力常数，数值大概是6.67×10^-11N·m2/kg2。
有了这个公式，理论上，只要我们知道两个物体的质量和它们之间的距离，就能算出引力。知道了引力F，根据牛顿第二定律F=ma就能求出物体的加速度a，进而知道物体的运动情况。
于是，一个完美的引力闭环就形成了。
我们终于可以同时掌握上游的引力计算，中游的引力转加速度以及下游的加速度分析运动了。
既然任督二脉已经打通，内循环也转了起来，要不，我们用牛刀杀一只鸡试试？
很多人在听万有引力故事时，都会听到牛顿被苹果砸到的事。这里我们不讨论故事的真伪，就单纯地分析一下苹果下落这个过程。
苹果为什么会下落？当然是因为受到了地球的引力，它是被地球“吸”向地心的。到了这里，相信大家对这个已经没啥异议了。
跟以前不同的是，我们现在已经知道了万有引力定律。
我们不仅知道苹果下落是由地球引力造成的，还能把这个引力的大小算出来。求出引力后，秉着“力是改变物体运动状（速度）”的想法，用牛顿第二定律F=ma把苹果下落的加速度a算出来，再根据加速度分析苹果的下落情况。
简单来说就是三步走：第一，找到让苹果下落的力（这里就是地球和苹果之间的引力，用万有引力定律来求）；第二，找到合外力后，用牛顿第二定律F=ma求苹果的加速度a；第三，利用加速度分析苹果下落的运动情况。
整个思路是如此的简单而清晰，我们一步步走。
第一步，找到苹果和地球之间的引力，这当然要求助于刚刚发现的万有引力定律：
从定律的形式来看，想知道苹果和地球之间的引力，就必须知道苹果的质量、地球的质量以及苹果与地球之间的距离r（G是个常数，不用管它），我们分别来看一看。
苹果的质量好说，你的苹果是半斤还是六两，称一称就知道了。不过，我们这里并不限定苹果的质量，大小随你挑，因为你很快就会发现苹果的下落情况跟苹果的质量压根没有关系。
这是一个让人非常吃惊的“巧合”，爱因斯坦就从这里撕开了通向广义相对论的一个口子。
小时候我们学过一篇《两个铁球同时着地》，说的也是这个事。同时放下一轻一重两个铁球，大家原以为重铁球会先着地，轻铁球后着地，结果发现它们居然是同时着地的。
