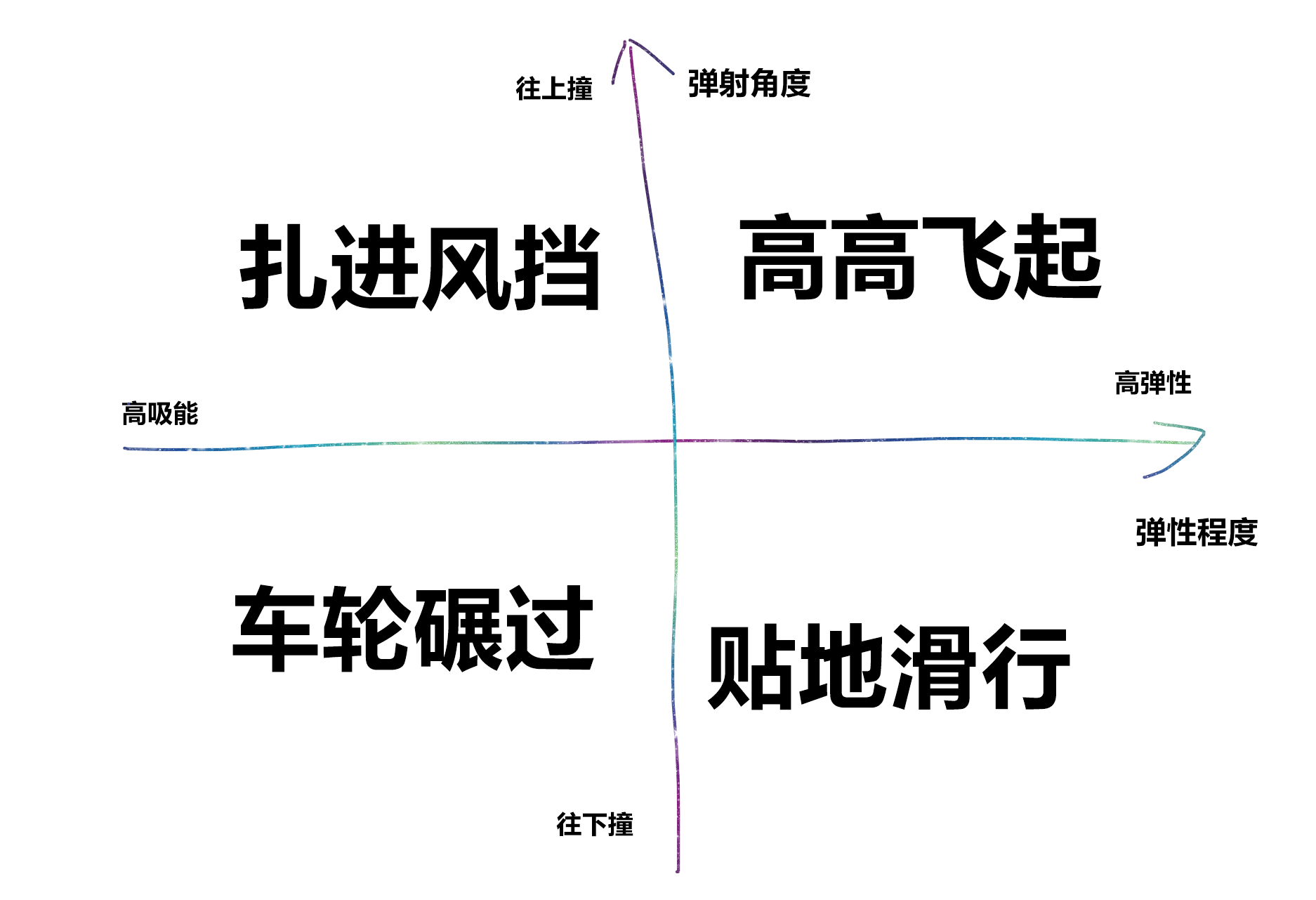
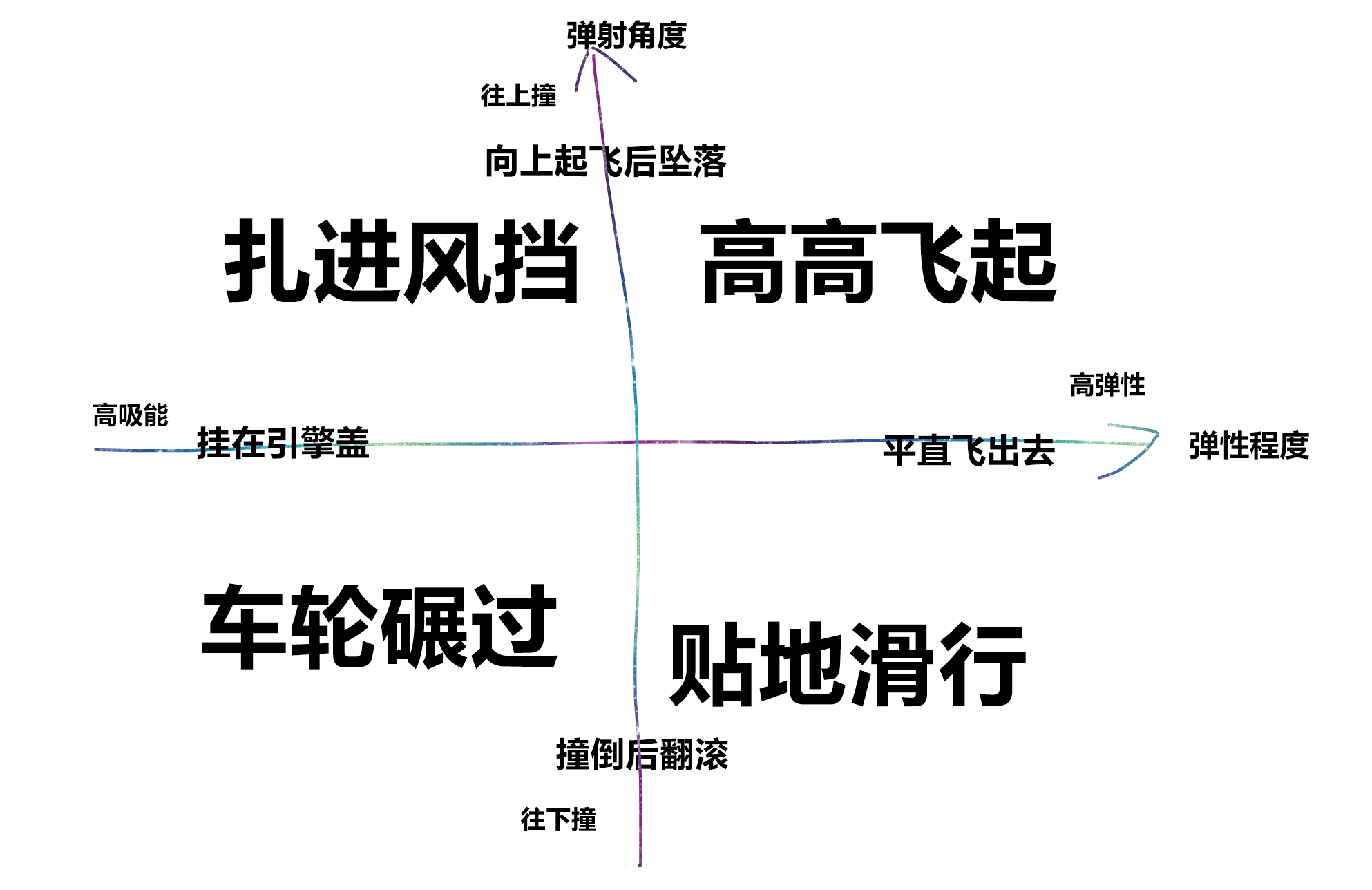
被汽车撞，会被撞飞还是碾过？

　　取决于什么呢？

　　取决于减肥是否成功

　　成功的飞起

　　失败的肉泥

　　取决于速度，质量，还有刹车距离。

　　速度太快

　　质量低速度足够快就会有撞飞的可能。质量比较大的不太会飞起来。

　　我考虑了一个极度简化的模型：假设人和车都是理想的刚体，忽略人体宽度的影响；正面碰撞，发生在一个点上并且是完全弹性碰撞；碰撞之前人相对于地面静止不动，如下图。碰撞点O可能是保险杠前端，也可能是引擎盖前端，反正就是车头某一点。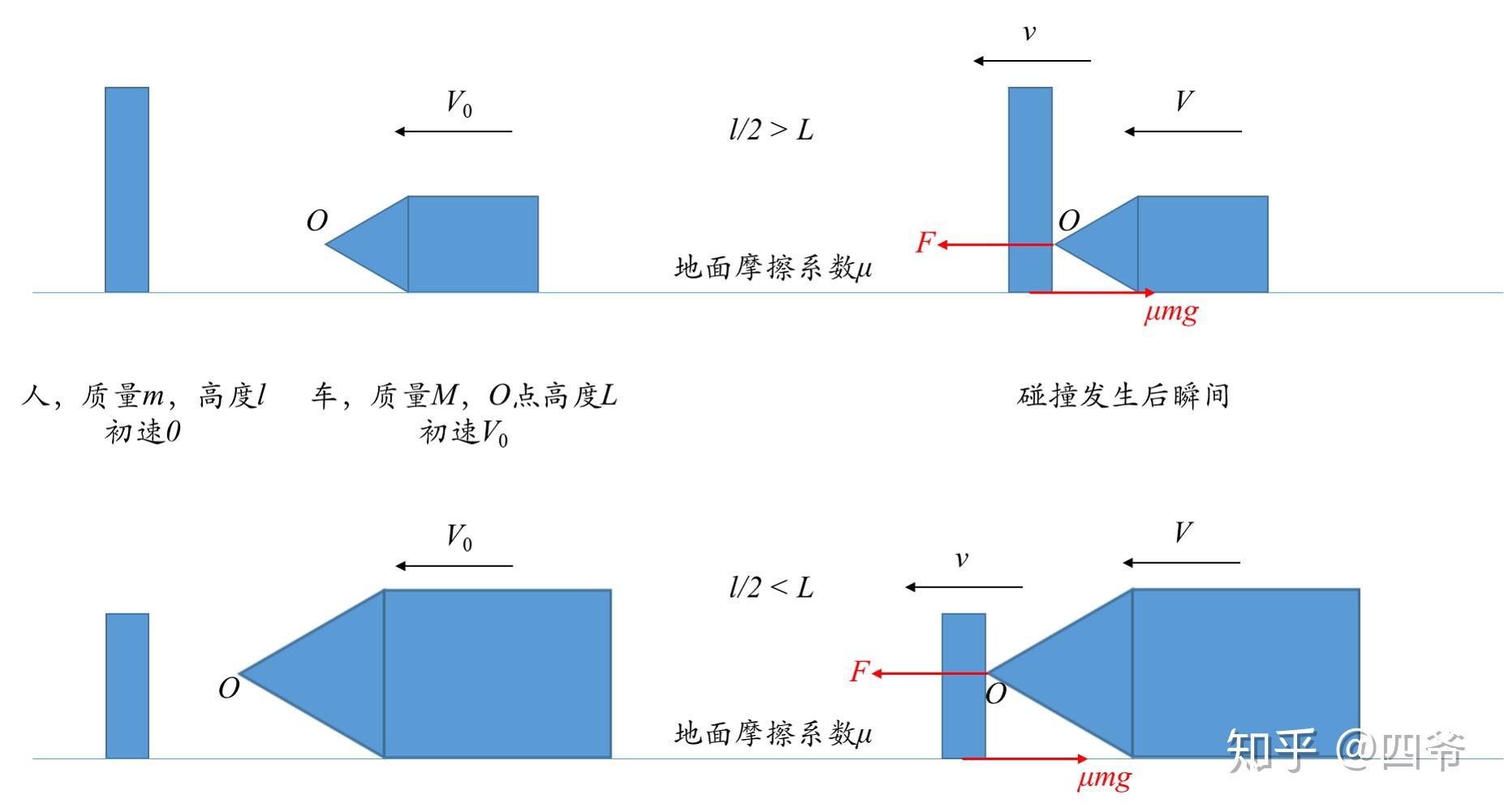PPT画的图，略丑请见谅

　　F是碰撞过程中的冲力，如果考察碰撞时间 \Delta t 的话，可以根据这里面的冲量关系 I=F·\Delta t=mv 把F算出来。人和地面间的摩擦力 f=\mu mg 。根据动量守恒 MV_0\ =\ MV\ +\ mv 和能量守恒 \frac{1}{2}MV_0^2\ =\ \frac{1}{2}MV^2\ +\ \frac{1}{2}mv^2 可以把碰撞后的速度算出来 V\ =\ \frac{M-m}{M+m}V_0，v\ =\ \frac{2M}{M+m}V_0=\ \frac{2}{1+\frac{m}{M}}V_0 。

　　理想情况下，冲力和摩擦力都作用于人的质心。

　　在 \frac{l}{2}≤L 时，也就是下半张图，冲力和摩擦力的力矩方向是一致的（ \frac{l}{2}=L 时，冲力的力臂是0，因此力矩也是0），都会使人逆时针旋转（狗头），也就是向前倒，然后被“碾过”。

　　上半张图，即 \frac{l}{2}>L 时，冲力和摩擦力的力矩方向相反，这就取决于谁更大了。冲力和摩擦力的力臂非别是 \frac{l}{2}-L，\frac{l}{2} ，那么力矩分别可表示为 M_F=F·\left(\frac{l}{2} -L\right)=\frac{mv}{\Delta t}·\left(\frac{l}{2} -L\right)=\frac{2mV_0}{\Delta t\left( 1+\frac{m}{M} \right)}·\left(\frac{l}{2} -L\right)，M_f=\frac{\mu mgl}{2} 。当 M_F 比较大时，总力矩将使人顺时针旋转，然后撞到引擎盖上被撞飞。反之，则和下半张图的情形类似，被碾过。而如果恰好 M_F=M_f ，那么总力矩为0，人会沿马路减速滑行（狗头×2）。

　　如果我们考虑这个比值 \frac{M_F}{M_f}=\frac{4}{g}·\frac{1}{\left( 1+\frac{m}{M} \right)}·\left( \frac{1}{2}-\frac{L}{l} \right)·\frac{V_0}{\ \mu \Delta t} ，可以得到一些定性的结论：一般来说，人身高越高、碰撞点（和人身高、车高都有关）越低、车速越快、地面越滑、碰撞时间越短，越容易发生“撞飞”的事故。

　　结合一点实际的话，如果“人”是小孩子，或者“车”是货车，那人就很容易被撞倒碾压，对应于前面那张图的下半部分。对于成年人和较小型的车辆来说，以一个身高1.7 m，体重60 kg的成年人为例，通常小轿车重约一两吨，这里取1.5 t（事实上由于通常m<<M， \frac{M_F}{M_f} 比值的第二项可以直接按1算），碰撞点假设在大腿部，约60 cm，再假设鞋底是橡胶的，普通橡胶和沥青路面的摩擦系数可以取0.25，重力加速度取海平面值的话，也就是 m=60\ kg，l=1.7\ m，M=1.5\ t，L=60\ cm，\mu=0.25，g=9.78 \ m/s^2 ，要使 \frac{M_F}{M_f}>1 的话，只要 \frac{V_0}{\Delta t}>4.3\ m/s^2 （这个值不是加速度的意思）。也就是说，如果碰撞时间 \Delta t 取 0.3\ s 的话，一辆小轿车的速度只要以 1.3\ m/s （和一般成年人步行速度差不多）的速度撞向一个成年人，就可以让这个人往引擎盖的方向倾倒；如果是正常行驶，比如时速40公里（约 11.1\ m/s ），就很有可能把人撞飞了。

　　注：以上提到的“人”都是开头假设里所述的“刚性人”。

　　顺带一提，这个 \Delta t 挺复杂的，跟很多因素有关，比如车速，再比如同样速度撞上大肚腩（不太刚性）的 \Delta t 肯定比撞上大肌霸（比较刚性）的 \Delta t 大一些。（注：此处的“刚性”和“阳刚”毫无关联。）

　　最后也是最重要的：珍爱生命，注意交通安全！

　　没有调查就没有发言权，作为一个实验学科的学生，我建议还是得多试，试个十来百把就能收集足够多的数据，然后把数据Plot一下就知道到底是撞飞还是碾过了。

　　我真踏马机智