归一化后和标准化后数据到底发生了什么变化？

　　原数据：

　　

　　 

　　一、归一化

　　

　　 

　　 

　　 

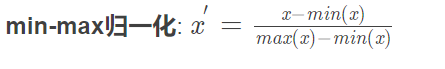
　　1)画图的时候限制xlim(-2,10)                                                                  2)画图的时候去掉xlim的限制

　　

　　 

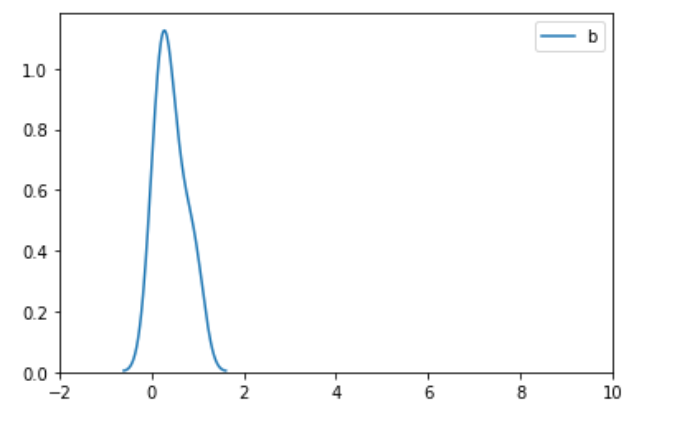
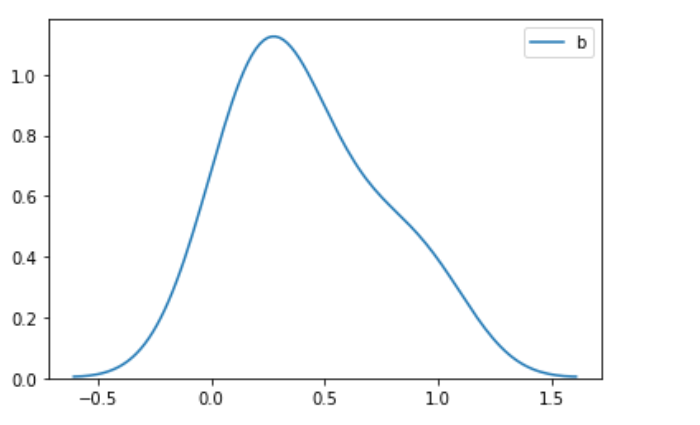
　　二、标准化

　　

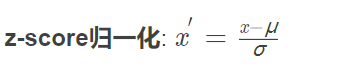
　　标准化后均值为0，方差为1.

　　1）限制xlim(-6,10)                                                                                                  2)去掉xlim限制

　　

　　 

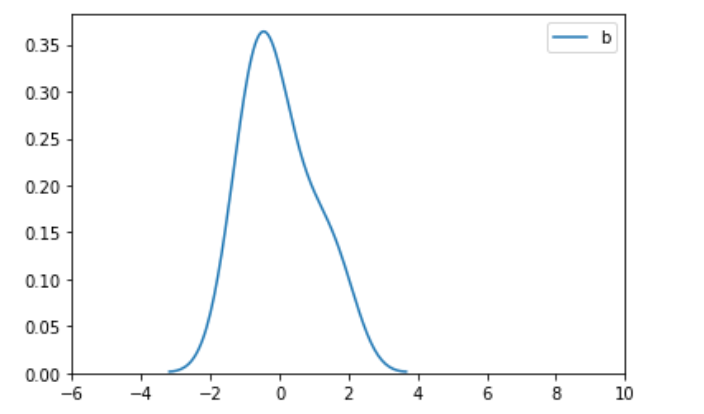
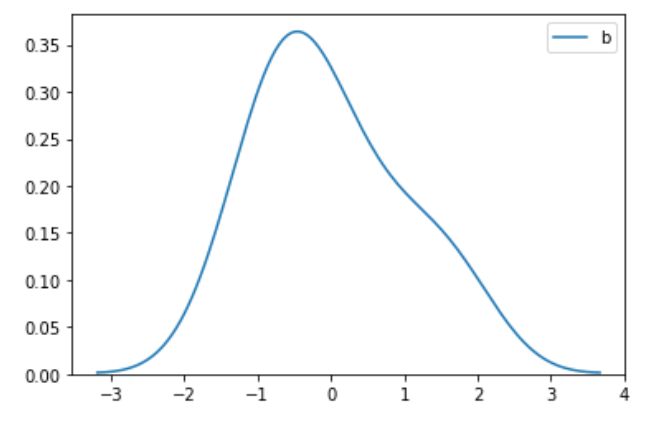
　　三、结论

　　从上述归一化和标准化可以看出来，转换后数据的均值和方差都发生了改变：

　　1）均值发生改变可以理解为数据的坐标都进行了平移转换，均值其实也是随之一样转换。

　　2）方差的改变是因为数据都压缩在了更小的范围内了，所以方差都变小了。

　　3）通过画图去掉xlim的限制，我们可以看出转换后的图的形状跟原图的形状是一样的，也就是图的形状本质上没变，只是压缩在更小的空间范围内，从同一xlim范围看是变瘦了。

　　 

　　四、什么时候使用标准化，什么时候使用归一化？

　　使用标准化

　　如果对数据无从下手可以直接使用标准化； 如果数据存在异常值和较多噪音，用标准化，可以间接通过中心化避免异常值和极端值的影响 需要使用距离来度量相似性的时候：比如k近邻、kmeans聚类、感知机和SVM，或者使用PCA降维的时候，标准化表现更好 使用归一化

　　数据较为稳定，不存在极值 在不涉及距离度量、协方差计算的时候，可以使用归一化方法 两者都不需要：

　　决策树、基于决策树的Boosting和Bagging等集成学习模型对于特征取值大小并不敏感 有较多类别变量的数据也是不需要做标准化处理的。 五、在机器学习中，标准化是更常用的手段，归一化的应用场景是有限的

　　标准化更好保持了样本间距。当样本中有异常点时，归一化有可能将正常的样本“挤”到一起去。比如三个样本，某个特征的值为1,2,10000，假设10000这个值是异常值，用归一化的方法后，正常的1,2就会被“挤”到一起去。如果不幸的是1和2的分类标签还是相反的，那么，当我们用梯度下降来做分类模型训练时，模型会需要更长的时间收敛，因为将样本分开需要更大的努力！而标准化在这方面就做得很好，至少它不会将样本“挤到一起”。 标准化更符合统计学假设。对一个数值特征来说，很大可能它是服从正态分布的。标准化其实是基于这个隐含假设，只不过是略施小技，将这个正态分布调整为均值为0，方差为1的标准正态分布而已。 举例看带有异常的归一化和标准化有什么区别：

　　

　　

　　 

　　

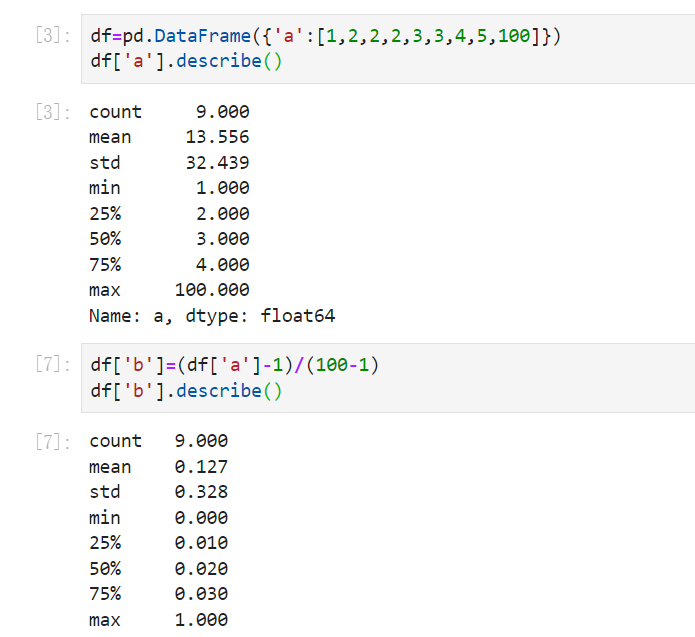
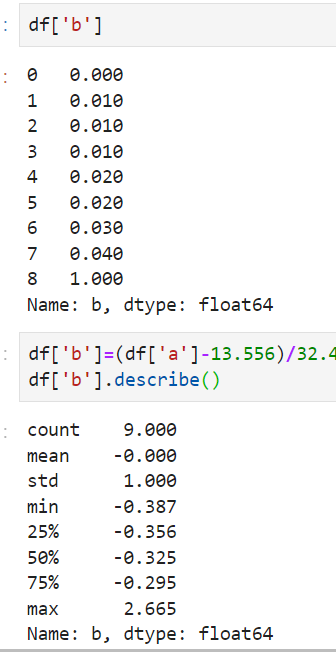
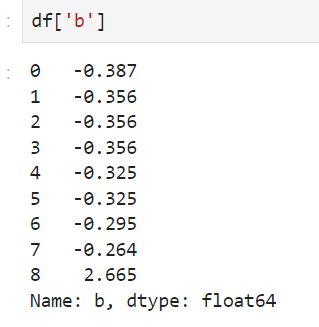
　　 从中可以看出，带有异常值的时候，min-max归一化后，把前面的数据都压缩到了很小的空间，相差100倍了，但是标准化后却差别没那么大，这就是标准化对异常值没那么敏感。

　　再看另外一组图片：

　　

　　 

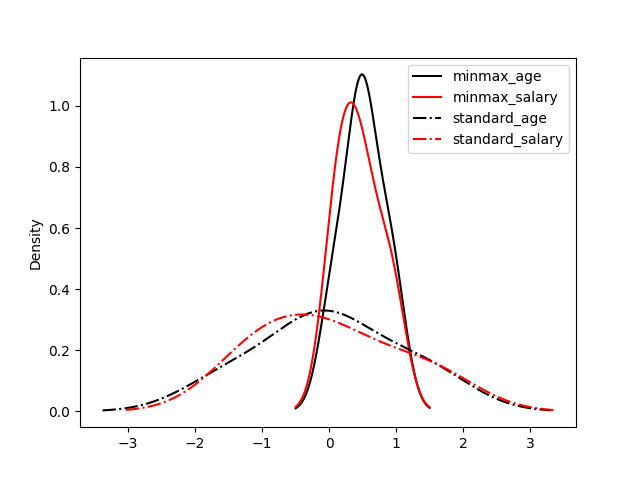
　　可以看出归一化比标准化方法产生的标准差小，使用归一化来缩放数据，则数据将更集中在均值附近。这是由于归一化的缩放是“拍扁”统一到区间（仅由极值决定），而标准化的缩放是更加“弹性”和“动态”的，和整体样本的分布有很大的关系。所以归一化不能很好地处理离群值，而标准化对异常值的鲁棒性强，在许多情况下，它优于归一化。

　　参考：https://zhuanlan.zhihu.com/p/450496701