【知识仓库】碰撞

时间：2022-10-28

　　有了动量守恒和能量守恒就可以来考虑几个刚体碰撞了。

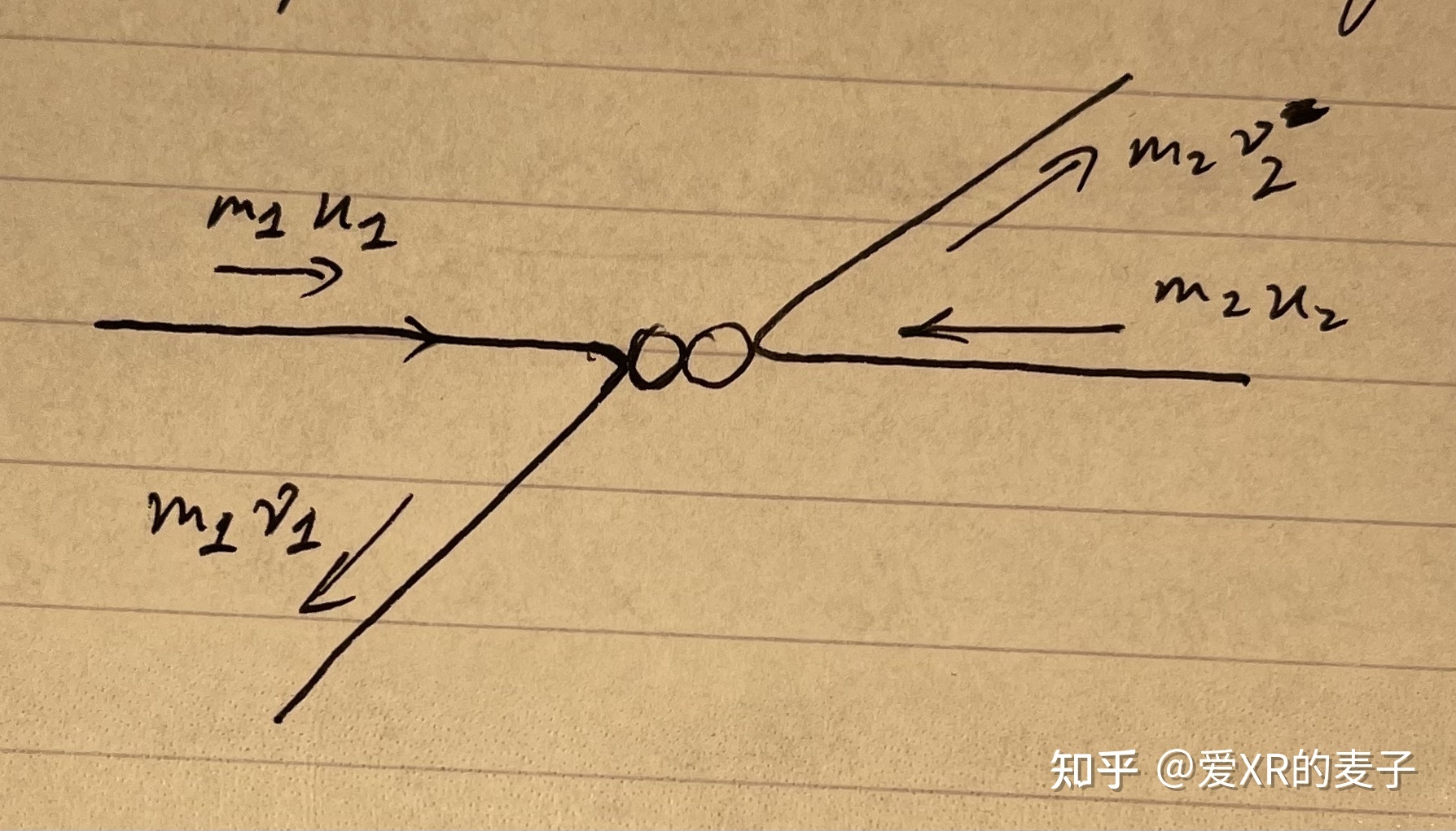
　　从最简单的情况考虑起，一个粒子质量为 $m_1$ ，移动速度为 $u_1$ ，另一个粒子质量 $m_2$ ，移动速度为 $u_2$ ，两个粒子运动方向相同，且 $u_2 < u_1$ ，因此两个粒子会发生碰撞。那么碰撞后，两粒子的速度是多少呢？

　　在思考这种情况时，我们需要做如下假设：

　　总动量 $p$ 是守恒的。因为 $dp = F dt$ ，动量守恒意味着外力和/或相互作用时间很小.势能可忽略。相互作用发生距离很短，因此势能在碰撞前后不发生改变。为了进一步简化思考，我们可以先假设是弹性碰撞 (Elastic Collision)，即总动能也守恒。因此便有了

　　 $m_1 v_1 + m_2 v_2 = m_1 u_1 + m_2 u_2 \\ m_1 v_1^2 + m_2 v_2^2 = m_1 u_1^2 + m_2 u_2^2$

　　做一些数学，不难得到

　　 $(v_2 - v_1)^2 = (u_2 - u_1)^2$

　　如果不考虑大家都为0，即不动的情况，以及速度保持原样， $v_i = u_i$ ，即不碰撞的情况。那么弹性碰撞前后粒子之间的相对速度是不变的。

　　 $\Rightarrow (v_2 - v_1) = -(u_2 - u_1)$

　　因此碰撞使得相对速度的方向改变了。

　　也可以解出两个末速度的表达

　　 $v_1 = (\frac{m_1 - m_2}{m_1 + m_2})u_1 + (\frac{2m_2}{m_1 + m_2})u_2 \\ v_2 = (\frac{2m_1}{m_1 + m_2})u_1 + (\frac{m_2 - m_1}{m_1 + m_2})u_2$

　　我们便能看出些运动规律。

　　如果我们认为 $m_2$ 作为目标一开始是不动的，即 $u_2 = 0$ 。那么

　　两个质量相同时， $m_1 = m_2$ ， $\Rightarrow v_1 = 0, v_2 = u_1$ ，粒子直接交换速度。如台球。目标质量大时， $\frac{m_2}{m_1} \rightarrow \infty$ ， $\Rightarrow v_1 = -u_1, v_2 = 0$ ，就像是 $m_1$ 撞上了一堵墙，直接反弹了。如 $\alpha$ 粒子撞击到金原子核的情况。目标质量小时， $\frac{m_2}{m_1} \rightarrow 0$ ， $\Rightarrow v_1 = u_1, v_2 = 2u_1$ ，这时 $m_1$ 就好像没受到影响一样继续向前，但是 $m_2$ 却被弹飞了。如将乒乓球置于篮球上方，然后同时下落，观察乒乓球的弹跳，会有别样的乐趣。如果上述碰撞，我们考虑质心是静止的。那么起始总动量和最终总动量都会是0。

　　 $m_1 v_1 + m_2 v_2 = 0 = m_1 u_1 + m_2 u_2$

　　如果

　　 $m_1 v_1 = -m_1 u_1 = m_2 u_2 = -m_2 v_2$

　　则能同时满足上面的式子和动能守恒。因此

　　在质心为参照系的时候，所有的粒子的动量都有相等的大小，碰撞只会影响方向而已。

　　我们可以随时转换到这个参照系里来，只要我们用起始的移动的速度减去质心的速度，进行计算，然后再用算出来的末速度加上这个质心的速度就可以了。

　　 $u_{CoM} = \frac{m_1 u_1 + m_2 u_2}{m_1 + m_2} = \frac{m_1 v_1 + m_2 v_2}{m_1 + m_2} = v_{CoM}$

　　将上面的式子换成向量表达式，便有了多维情况的碰撞

　　 $m_1 \vec v_1 + m_2 \vec v_2 = m_1 \vec u_1 + m_2 \vec u_2 \\ m_1 v_1^2 + m_2 v_2^2 = m_1 u_1^2 + m_2 u_2^2$

　　而 $v_i^2 = \vec v_i \cdot \vec v_i$ 。

　　我们可以发现，这里有4个式子，却又6个未知量（一个向量有三个），因此我们需要更多的信息，例如 $\vec v_1, \vec v_2$ 所在平面和两者其中一个的角度。

　　不论如何，我们都能得到与一维类似的情况

　　 $\left$

　　两个粒子间的相对速度不变，会变的只有方向。

　　当采用质心为参照系的时候，总动量为0，所以

　　 $m_1 \vec u_1 = - m_2 \vec u_2, m_1 \vec v_1 = - m_2 \vec v_2$ ，

　　而所有动量的大小都一样。

　　这隐含了，在质心参照系中，每个粒子在碰撞前后都有相同的速度，但是方向会发生改变。碰撞的一些细节将所有动量方向旋转了一个角度而已。

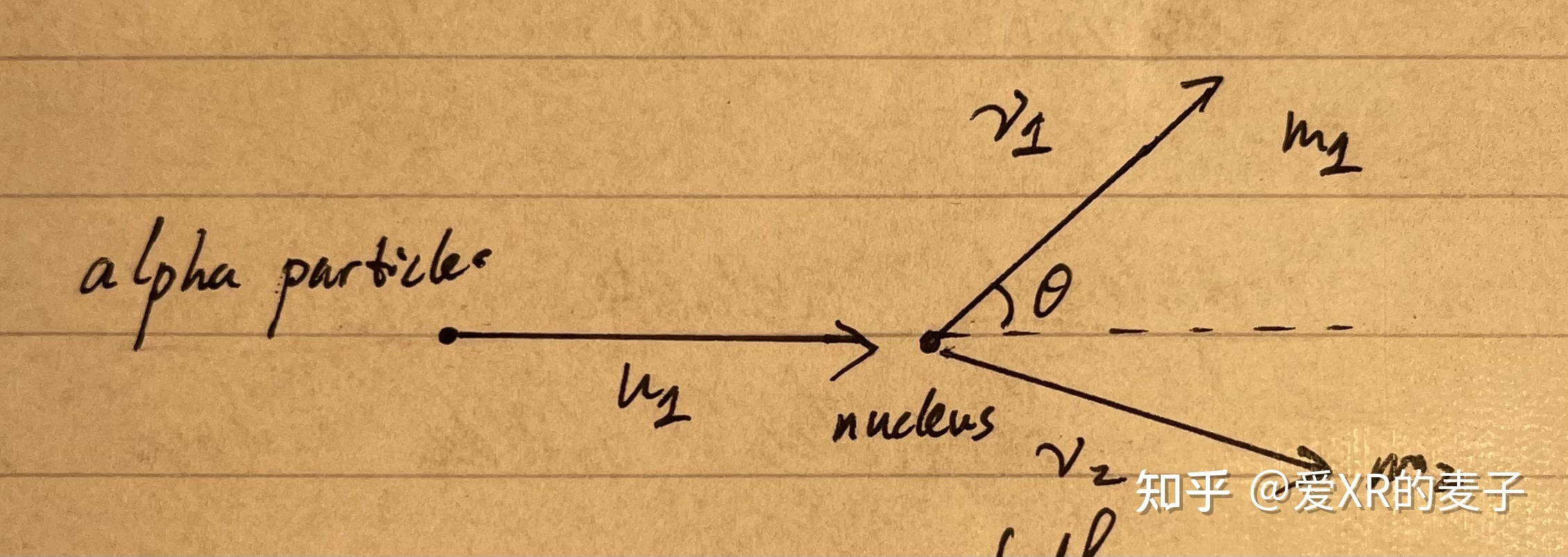
　　欧内斯特·卢瑟福 (Ernest Rutherford)将 $\alpha$ 粒子（氦原子核， $m_{\alpha} = 4 m_p$ ）打向金箔（ $m_{Au} = 197 m_p$ ）。其中 $\frac{1}{8000}$ 的 $\alpha$ 粒子基本上以 $180^\circ$ 的角度反弹了回来。由此卢瑟福推断出了原子核的存在并相信它饱含了一个原子绝大部分的质量。

　　假如通过实验，我们可以得到 $u_1$ ， $v_1$ 以及 $\theta$ 。同时我们认为原子核一开始是静止的，即 $\vec u_2 = \vec 0$ 。我们可以从中计算出原子核的质量， $m_2$ 。

　　动量守恒，所以 $m_1 \vec u_1 = m_1 \vec v_1 + m_2 \vec v_2$ ，

　　 $\Rightarrow m_2 \vec v_2 = m_1 (\vec u_1 - \vec v_1) \\ \Rightarrow m_2^2 v_2^2 = m_1^2 \left$

　　而动能守恒给了我们

　　 $m_1 u_1^2 = m_1 v_1^2 + m_2 v_2^2 \\ \Rightarrow m_2 v_2^2 = m_1 (u_1^2 - v_1^2)$

　　因此

　　 $m_2 = m_1 \frac{\left$

　　 $\Rightarrow \frac{m_2}{m_1} = \frac{u_1^2 + v_1^2 - 2u_1 v_1 cos(\theta)}{u_1^2 - v_1^2}$

　　当完全反弹的时候， $\theta = 180^\circ$ ， $\Rightarrow cos(\theta) = -1$

　　 $\Rightarrow \frac{m_2}{m_1} = \frac{u_1^2 + v_1^2 + 2u_1 v_1}{u_1^2 - v_1^2} = \frac{u_1 + v_1}{u_1 - v_1}$

　　而卢瑟福在实验中发现， $\alpha$ 粒子的能量基本没发生变化，因此 $u_1 \approx v_1$ ，就有了 $m_2 \gg m_1$ 。因此金原子大部分的质量都集中在了很小的空间中。

　　虽然动量一直守恒，但是动能却有可能损耗掉，比如汽车碰撞中产生的热量。但是并不是全部的动能都可以被损耗掉，因为动量守恒意味着还存在移动。

　　最极端的情况被称作完全非弹性碰撞 (Completely Inelastic Collision)。在质心参照系中，两个粒子碰撞，损耗掉了全部的动能，并作为了一个粒子存在。

　　而在实验室参照系中（就是一般视角的参照系），最终的末速度将是质心移动的速度

　　 $\vec v = \frac{m_1 \vec u_1 + m_2 \vec u_2}{m_1 + m_2}$ ，

　　而一般的非弹性碰撞则介于弹性碰撞与完全非弹性碰撞之间。